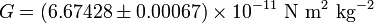LEY DE GRAVITACION
La ley de la Gravitación Universal es una ley física clásica que describe la interacción gravitatoria entre distintos cuerpos con masa. Ésta fue presentada por Isaac Newton en su libro Philosophiae Naturalis Principia Mathematica, publicado en 1687, donde establece por primera vez una relación cuantitativa (deducida empíricamente de la observación) de la fuerza con que se atraen dos objetos con masa. Así, Newton dedujo que la fuerza con que se atraen dos cuerpos de diferente masa únicamente depende del valor de sus masas y del cuadrado de la distancia que los separa. También se observa que dicha fuerza actúa de tal forma que es como si toda la masa de cada uno de los cuerpos estuviese concentrada únicamente en su centro, es decir, es como si dichos objetos fuesen únicamente un punto, lo cual permite reducir enormemente la complejidad de las interacciones entre cuerpos complejos.
Así, con todo esto resulta que la ley de la Gravitación Universal predice que la fuerza ejercida entre dos cuerpos de masas  y
y  separados una distancia
separados una distancia  es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia, es decir
es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia, es decir
(1)
donde
-
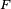 es el módulo de la fuerza ejercida entre ambos cuerpos, y su dirección se encuentra en el eje que une ambos cuerpos.
es el módulo de la fuerza ejercida entre ambos cuerpos, y su dirección se encuentra en el eje que une ambos cuerpos. -
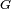 es la constante de la Gravitación Universal.
es la constante de la Gravitación Universal.
Es decir, cuanto más masivos sean los cuerpos y más cercanos se encuentren, con mayor fuerza se atraerán. El valor de esta constante de Gravitación Universal no pudo ser establecido por Newton, que únicamente dedujo la forma de la interacción gravitatoria, pero no tenía suficientes datos como para establecer cuantitativamente su valor. Únicamente dedujo que su valor debería ser muy pequeño. Sólo mucho tiempo después se desarrollaron las técnicas necesarias para calcular su valor, y aún hoy es una de las constantes universales conocidas con menor precisión. En 1798 se hizo el primer intento de medición(véase el experimento de Cavendish) y en la actualidad, con técnicas mucho más precisas se ha llegado a estos resultados:
(2)
en unidades del Sistema Internacional.
Esta ley recuerda mucho a la forma de la ley de Coulomb para las fuerzas electrostáticas, ya que ambas leyes siguen una ley de la inversa del cuadrado (es decir, la fuerza decae con el cuadrado de la distancia) y ambas son proporcionales al producto de magnitudes propias de los cuerpos (en el caso gravitatorio de sus masas y en el caso electrostáticos de su carga eléctrica).
Aunque actualmente se conocen los límites en los que dicha ley deja de tener validez (lo cual ocurre básicamente cuando nos encontramos cerca de cuerpos extremadamente masivos), en cuyo caso es necesario realizar una descripción a través de la Relatividad General enunciada por Albert Einstein en 1915, dicha ley sigue siendo ampliamente utilizada y permite describir con una extraordinaria precisión los movimientos de los cuerpos (planetas, lunas, asteroides, etc) del Sistema Solar, por lo que a grandes rasgos, para la mayor parte de las aplicaciones cotidianas sigue siendo la utilizada, debido a su mayor simplicidad frente a la Relatividad General, y a que ésta en estas situaciones no predice variaciones detectables respecto a la Gravitación Universal.
Trabajos de Hooke y disputa
Cuando el primer libro de los Principios de Newton fue expuesto a la Royal Society (la Real Academia de las Ciencias, de Inglaterra), el coetáneo Robert Hooke acusó a Newton de plagio por copiarle la idea de que la gravedad decaía como la inversa cuadrado de la distancia entre los centros de ambos cuerpos. Aunque esta controversia ha durado incluso hasta nuestros días, no hay datos claros sobre si realmente Newton conocía los trabajos de Hooke o no, ya que aunque ambos se carteaban regularmente, en ninguna de esas cartas Hooke menciona la ley de la inversa cuadrado, algo que Newton sí hizo con otros autores a los que sí agradeció[1] los trabajos anteriores en los que basó sus ideas. Frente a esta proclama de Hooke de su idea de la inversa cuadrado, Newton reiteró que dicha idea en ningún caso era exclusivamente de él, sino que fueron varios autores en aquella época que ya se dieron cuenta de una dependencia de ese tipo, como reflejó en los agradecimientos de su publicación.
Relación con las Leyes de Kepler
Las Leyes de Kepler (enunciadas por Johannes Kepler) eran una serie de tres leyes empíricas que describían el movimiento de los planetas a través de las observaciones existentes. Aunque éstas describían dichos movimientos, los motivos de por qué éstos eran así o qué los causaban permanecían desconocidas tanto para Kepler como para sus coetáneos. Sin embargo, éstas supusieron un punto de partida para Newton, quien pudo dar una formulación matemática a dichas leyes, lo cual junto con sus propios logros condujeron a la formulación de la ley de la Gravitación Universal. En especial, a través de dicha ley Newton pudo dar la forma completa a la Tercera ley de Kepler, que describe que los cuadrados de los periodos de las órbitas de los planetas son proporcionales a los cubos de sus distancias al Sol. Es decir, que los planetas más alejados del Sol tardan más tiempo en dar una vuelta alrededor de éste (su año es más largo).
Formulación general de la ley de la Gravitación Universal
Forma vectorial
Aunque en la ecuación () se ha detallado la dependencia del valor de la fuerza gravitatoria para dos cuerpos cualesquiera, existe una forma más general con la que poder describir completamente dicha fuerza, ya que en lugar de darnos únicamente su valor, también podemos encontrar directamente su dirección. Para ello, se convierte dicha ecuación en forma vectorial, para lo cual únicamente hay que tener en cuenta las posiciones donde se localizan ambos cuerpos, referenciados a un sistema de referencia cualquiera. De esta forma, suponiendo que ambos cuerpos se encuentran en las posiciones  , la fuerza (que será un vector ahora) vendrá dada por
, la fuerza (que será un vector ahora) vendrá dada por
(2)
donde  es el vector unitario que va del centro de gravedad del objeto 1 al del objeto 2.
es el vector unitario que va del centro de gravedad del objeto 1 al del objeto 2.
Cuerpos extensos
Se ha mencionado anteriormente que dichos cuerpos se pueden tratar como cuerpos puntuales, localizados en el centro de gravedad del cuerpo real, de tal forma que la descripción de esta fuerza se realiza trabajando únicamente con cuerpos puntuales (toda su masa se encuentra concentrada en su centro). Sin embargo, para algunos casos se puede hacer necesario tratar dichos cuerpos como lo que son, cuerpos con una extensión dada, es decir no puntuales. Un ejemplo donde este tratamiento es obligatorio es cuando se desea determinar cómo varía la fuerza de la gravedad a medida que nos situamos en el interior de un objeto, por ejemplo qué gravedad existe en el interior de la Tierra (en la región del manto terrestre o del núcleo).
En estos casos es necesario describir al objeto masivo como una distribución de masa, es decir describirlo a través de su densidad en cada punto del espacio. Así, se integra la fuerza que produce cada elemento infinitesimal del cuerpo sobre cada elemento del otro objeto, sumando a todos los elementos que existen en el volumen de ambos cuerpos, lo cual matemáticamente se traduce en una integral sobre el volumen de cada cuerpo, de tal forma que la fuerza gravitatoria entre ambos se obtiene como
(3)
Donde
-
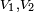 son los volúmenes de los dos cuerpos.
son los volúmenes de los dos cuerpos. -
 son las densidades de los dos cuerpos en cada punto del espacio (
son las densidades de los dos cuerpos en cada punto del espacio ( ).
).
Puede verse que si se tienen dos cuerpos finitos entonces la fuerza gravitatoria entre ambos viene acotada por:
Donde  son las distancias mínima y máxima entre los dos cuerpos en un instante dado.
son las distancias mínima y máxima entre los dos cuerpos en un instante dado.
Relación del peso de un cuerpo con la fuerza centrífuga de la tierra
Cuando un cuerpo describe un movimiento circular su velocidad va cambiando constantemente de dirección, motivo por el cual decimos que tiene una aceleración, no obstante que la magnitud de la velocidad no cambie. La aceleración que sufre el cuerpo se debe a una fuerza que actúa en forma constante, a lo largo de un radio, hacia el centro del círculo, dicha fuerza recibe el nombre de fuerza centrípeta. Si esta fuerza deja de actuar, el cuerpo sale disparado en forma tangencial a la curva, siguiendo un movimiento rectilíneo uniforme como resultado de la inercia del cuerpo que tratará de seguir en movimiento.
Si se pone a girar una piedra atada a un cordel, este ejerce una fuerza centrípeta constante para jalar a la piedra acelerándola hacia el centro del círculo. La piedra ejerce sobre el cordel una fuerza centrífuga que la impulsa hacia afuera, originando una tensión en el cordel que aumentará a medida que sea mayor la velocidad con que gira la piedra. La magnitud de la fuerza centrípeta es igual a la de la fuerza centrífuga pero actúan en sentidos opuestos. Para calcular el valor de la fuerza centrípeta o la fuerza centrífuga se usa la ecuación:
Donde:
Fc= Fuerza centrípeta o centrífuga en N
m= Masa del cuerpo que gira en kg
v= Velocidad lineal del cuerpo en m/s
r= Radio de la circunferencia en m
La fuerza centrífuga que produce el movimiento de la Tierra es mayor en el ecuador que en los polos. Esto se debe a que en un punto del ecuador se mueve más rápido que uno próximo a los polos. Por tanto, cuando la Tierra da una vuelta al rededor de su eje, el punto sobre el ecuador habrá recorrido aproximadamente 40,000 km, que es el valor de la longitud de la circunferencia en el ecuador, mientras que el punto próximo a uno de los polos recorrería aproximadamente 1000 km. Debido a ello, la velocidad lineal en el ecuador será mayor que cerca de los polos y consecuentemente será mayor también su fuerza centrífuga. Como la fuerza centrífuga actúa sobre los cuerpos tratando de alejarlos del centro del giro, la fuerza centrífuga de la Tierra empuja a los cuerpos alejándolos de su centro, reduciendo el efecto de la fuerza de gravedad.
En general: un cuerpo tiene mayor peso cerca de los polos que en el ecuador, toda vez que la fuerza centrífuga que trata de separarlo de la superficie es menor, además de encontrarse más cerca del centro de la Tierra debido al achatamiento de sus polos.
Consecuencias
Aceleración de la gravedad
Considerando la Segunda ley de Newton, que explica que la aceleración que sufre un cuerpo es proporcional a la fuerza ejercida sobre él, estando relacionadas por una constante de proporcionalidad que es precisamente la masa de dicho objeto,
e introduciéndolo en la ley de la Gravitación Universal (en su forma más simple, únicamente por simplicidad) se obtiene que la aceleración que sufre un cuerpo debido a la fuerza de la gravedad ejercida por otro de masa  es igual a
es igual a
donde  es la aceleración sufrida. Es decir, dicha aceleración es independiente de la masa que presente nuestro objeto, únicamente depende de la masa del cuerpo que ejerce la fuerza y de su distancia. Por ello, si se tienen dos cuerpos de diferente masa (por ejemplo la Luna y un satélite artificial, que únicamente tenga una masa de unos pocos kilogramos) a la misma distancia de la Tierra, la aceleración que produce ésta sobre ambos es exactamente la misma. Como esta aceleración tiene la misma dirección que la de la fuerza, es decir en la dirección que une ambos cuerpos, esto produce que si sobre ambos cuerpos no se ejerce ninguna otra fuerza externa, éstos se moverán describiendo órbitas entre sí, lo cual describe perfectamente el movimiento planetario (o del sistema Tierra—Luna), o de caída libre aproximándose un cuerpo hacia el otro, como ocurre con cualquier objeto que soltemos en el aire y que cae irremediablemente hacia el suelo, en la dirección del centro de la Tierra.
es la aceleración sufrida. Es decir, dicha aceleración es independiente de la masa que presente nuestro objeto, únicamente depende de la masa del cuerpo que ejerce la fuerza y de su distancia. Por ello, si se tienen dos cuerpos de diferente masa (por ejemplo la Luna y un satélite artificial, que únicamente tenga una masa de unos pocos kilogramos) a la misma distancia de la Tierra, la aceleración que produce ésta sobre ambos es exactamente la misma. Como esta aceleración tiene la misma dirección que la de la fuerza, es decir en la dirección que une ambos cuerpos, esto produce que si sobre ambos cuerpos no se ejerce ninguna otra fuerza externa, éstos se moverán describiendo órbitas entre sí, lo cual describe perfectamente el movimiento planetario (o del sistema Tierra—Luna), o de caída libre aproximándose un cuerpo hacia el otro, como ocurre con cualquier objeto que soltemos en el aire y que cae irremediablemente hacia el suelo, en la dirección del centro de la Tierra.
Con esta ley se puede determinar la aceleración de la gravedad que produce un cuerpo cualquiera situado a una distancia dada. Por ejemplo, se deduce que la aceleración de la gravedad que nos encontramos en la superficie terrestre debido a la masa de la Tierra es de  , que es la aceleración sufrida por un objeto al caer. Y que esta aceleración es prácticamente la misma en el espacio, a la distancia donde se encuentra la Estación Espacial Internacional,
, que es la aceleración sufrida por un objeto al caer. Y que esta aceleración es prácticamente la misma en el espacio, a la distancia donde se encuentra la Estación Espacial Internacional,  (es decir, es un 95% de la gravedad que tenemos en la superficie, únicamente una diferencia de un 5%), siendo necesario recordar que el hecho de que los astronautas no sientan la gravedad no es porque ésta allí sea nula, sino por su estado de ingravidez (de caída libre continua). Y la gravedad que ejerce una persona sobre otra, situada a un metro de distancia, es de en torno a
(es decir, es un 95% de la gravedad que tenemos en la superficie, únicamente una diferencia de un 5%), siendo necesario recordar que el hecho de que los astronautas no sientan la gravedad no es porque ésta allí sea nula, sino por su estado de ingravidez (de caída libre continua). Y la gravedad que ejerce una persona sobre otra, situada a un metro de distancia, es de en torno a  (para una persona de unos 100 kg). Este es el hecho por el que no sentimos la gravedad que ejercen cuerpos poco masivos como nosotros.
(para una persona de unos 100 kg). Este es el hecho por el que no sentimos la gravedad que ejercen cuerpos poco masivos como nosotros.
Preferencia del cuerpo más masivo
Continuando con lo que se acaba de mencionar acerca de la aceleración que sufre un cuerpo como consecuencia de otro objeto masivo, el hecho de que esta aceleración únicamente dependa de la masa de este cuerpo (olvidándonos de su distancia por un momento) muestra que para dos cuerpos dados de diferente masa, el cuerpo menos masivo será el que sufra una aceleración mayor, y por tanto un movimiento más pronunciado. Con esto se observa directamente una respuesta a por qué es la Tierra la que orbita en torno al Sol y no al revés, puesto que este último tiene una masa increíblemente superior a la de la Tierra (unas 330.000 veces superior), haciendo que el movimiento sufrido por el Sol como consecuencia de la Tierra sea insignificante. Y de igual modo, es la Luna (cuerpo menos masivo) quien orbita en torno a la Tierra.
Interior de un cuerpo esférico
Una de las consecuencias que trae que la gravedad sea una fuerza que depende como la inversa del cuadrado de la distancia es que si se tiene un cuerpo esférico, con una densidad que únicamente va variando a medida que nos alejamos del centro del cuerpo (lo cual podría ser un modelo que describe de forma bastante adecuada a la Tierra), se puede demostrar a través de la ley de Gauss que la fuerza en su interior (a una distancia  del centro) únicamente depende de la masa existente dentro de la esfera de radio
del centro) únicamente depende de la masa existente dentro de la esfera de radio  . Es decir, la masa que hay fuera de dicha esfera no produce ninguna fuerza sobre un cuerpo situado en dicho punto. Por ello, dentro del cuerpo la fuerza ya no depende de la inversa cuadrado (puesto que ahora la masa a considerar depende también de dicha distancia) y resulta que es proporcional a dicha distancia. Esto es, en el interior del cuerpo la fuerza de la gravedad va creciendo conforme nos alejamos del centro del cuerpo (en donde ésta es nula) hasta llegar a la superficie, donde se hace máxima. A partir de aquí se observa el comportamiento habitual de decrecimiento conforme nos alejamos del cuerpo. Todo esto se puede ver en mayor profundidad en la entrada de la intensidad del campo gravitatorio.
. Es decir, la masa que hay fuera de dicha esfera no produce ninguna fuerza sobre un cuerpo situado en dicho punto. Por ello, dentro del cuerpo la fuerza ya no depende de la inversa cuadrado (puesto que ahora la masa a considerar depende también de dicha distancia) y resulta que es proporcional a dicha distancia. Esto es, en el interior del cuerpo la fuerza de la gravedad va creciendo conforme nos alejamos del centro del cuerpo (en donde ésta es nula) hasta llegar a la superficie, donde se hace máxima. A partir de aquí se observa el comportamiento habitual de decrecimiento conforme nos alejamos del cuerpo. Todo esto se puede ver en mayor profundidad en la entrada de la intensidad del campo gravitatorio.
Interior de una corteza hueca
Y por extensión de lo que se acaba de mencionar, en el caso en que se tuviese un cuerpo esférico pero hueco por dentro (es decir que únicamente sería unas cáscara esférica), en cualquier punto externo a él sigue produciendo una fuerza de la gravedad de acuerdo con la ecuación (), es decir como si dicho cuerpo fuese puntual. Sin embargo, al adentrarnos dentro del mismo, observaríamos cómo no hay fuerza de la gravedad, puesto que en su interior ya no hay masa.
Movimiento de los planetas
Como se ha mencionado en el apartado histórico, esta ley permite recuperar y explicar la Tercera Ley de Kepler, que muestra de acuerdo a las observaciones que los planetas que se encuentran más alejados del Sol tardan más tiempo en dar una vuelta alrededor de éste. Además de esto, con dicha ley y usando las leyes de Newton se describe perfectamente tanto el movimiento planetario del Sistema Solar como el movimiento de los satélites (lunas) o sondas enviadas desde la Tierra. Por ello, esta ley estuvo considerada como una ley fundamental por más de 200 años, y aún hoy sigue estando vigente para la mayoría de los cálculos necesarios que atañen a la gravedad.
Uno de los hechos que muestran su precisión es que al analizar las órbitas de los planetas conocidos en torno a 1800 (en donde quedaban por descubrir Neptuno y Plutón), se observaban irregularidades en torno a la órbita de Urano principalmente, y de Saturno y Júpiter en menor medida, respecto a lo que predecía la ley de Newton (junto con las leyes de Kepler). Por esta razón, algunos astrónomos supusieron que dichas irregularidades eran debidas a la existencia de otro planeta más externo, alejado, que todavía no había sido descubierto. Así, tanto Adams como Le Verrier (de forma independiente) calcularon matemáticamente dónde debería encontrarse dicho planeta desconocido para poder explicar dichas irregularidades. Neptuno fue descubierto al poco tiempo por el astrónomo Galle, el 23 de septiembre de 1846, siguiendo sus indicaciones y encontrándolo a menos de un grado de distancia de la posición predicha.
Limitaciones
Si bien la ley de la gravitación universal da una muy buena aproximación para describir el movimiento de un planeta alrededor del Sol, o de un satélite artificial relativamente cercano a la Tierra, durante el siglo XIX se observó algunos pequeños problemas que no se conseguían resolver (similares al de las órbitas de Urano, que sí pudo resolverse tras el descubrimiento de Neptuno). En especial, se encontraba la órbita del planeta Mercurio, la cual en lugar de ser una elipse cerrada, tal y como predecía la teoría de Newton, es una elipse que en cada órbita va rotando, de tal forma que el punto más cercano al Sol (el perihelio) se desplaza ligeramente, unos 43 segundos de arco por siglo, en un movimiento que se conoce como precesión. Aquí, al igual que con el caso de Urano, se postuló la existencia de un planeta más interno al Sol, al cual se le llamó Vulcano, y que no habría sido observado por estar tan próximo al Sol y quedar oculto por su brillo. Sin embargo, éste planeta no existe en la realidad (su existencia era inviable de todas formas), por lo que dicho problema no pudo resolverse, hasta la llegada de la Relatividad General de Einstein.
Además de este problema, en la actualidad el número de las desviaciones observacionales existentes que no se pueden explicar bajo la teoría newtoniana son varias:
- Como se ha mencionado ya, la trayectoria del planeta Mercurio no es una elipse cerrada tal como predice la teoría de Newton, sino una cuasi-elipse que gira secularmente, produciendo el problema del avance del perihelio que fue explicado por primera vez sólo con la formulación de la teoría general de la relatividad. Esta discrepancia obedece precisamente al límite de validez que actualmente conocemos para la teoría de Newton: ésta únicamente es válida para cuerpos de poca masa o distancias grandes, lo cual se cumple para todos los planetas del Sistema Solar excepto para Mercurio, puesto que éste se encuentra muy cercano al Sol, un cuerpo lo suficientemente masivo para producir discrepancias observables (aunque recordando que dicha discrepancia es únicamente un efecto de 46 segundos de arco por siglo, el uso de la Relatividad General sigue siendo necesario exclusivamente para cálculos de alta precisión).
- Aunque bajo la descripción de la gravedad de Newton ésta únicamente se produce entre cuerpos con masa, se ha observado cómo la luz también se curva (se desvía) como consecuencia de la gravedad producida por un cuerpo masivo, por ejemplo el Sol. Este hecho, que aunque sí podía llegar a interpretarse únicamente usando la ley de la Gravitación Universal, ésta no daba cuenta de la desviación correcta observada, resultó ser una de las primeras predicciones contrastadas que apoyaron la Relatividad General.
- La velocidad de rotación de las galaxias no parece responder adecuadamente a la ley de la gravitación, lo que ha llevado a formular el problema de la materia oscura y alternativamente de la dinámica newtoniana modificada. A través de la Tercera ley de Kepler hemos mencionado que los periodos de los cuerpos crecen con la distancia a la que se encuentran del cuerpo masivo. Aplicando dicho principio a las estrellas de una galaxia, debería observarse algo similar para las estrellas más alejadas del centro de la galaxia, pero esto es algo que no se observa y que, manteniendo la ley de la Gravitación Universal, únicamente puede ser explicado si en dicha galaxia existe mucha más masa de la que se observa, la cual es precisamente la denominada materia oscura, puesto que sería materia que no vemos.
Problemas filosóficos
Acción a distancia
A parte de los problemas prácticos mencionados anteriormente, existían algunos problemas de carácter más filosófico que atañen a la propia teoría en sí. En concreto, uno de ellos era el concepto de acción a distancia que utiliza la teoría. Esto es, en todo momento se ha descrito que dos cuerpos alejados una determinada distancia (y por tanto, no se encuentran en contacto entre sí) se ejercen una fuerza, la fuerza de la gravedad. Sin embargo, sería necesario responder a las preguntas de ¿cómo se ejerce dicha fuerza si ambos cuerpos no se tocan?. Esto era una cuestión por resolver, no únicamente de la teoría de Newton, sino que también atañía al electromagnetismo, y que no se sabía cómo afrontar. Por ello, esto dio lugar al concepto físico de campo, que aunque no resolvía completamente el problema, sí facilitaba la utilización de estas fuerzas a distancia y su explicación, y que para la gravedad hizo que se comenzase a trabajar a través de la idea del campo gravitatorio como causante de dicha fuerza de la gravedad.
Posteriormente, este problema quedaría resuelto en la Relatividad General, ya que en ésta se prescindió de describir la gravedad como una fuerza, pasando a entenderse ésta como una consecuencia de que los cuerpos con masa curvan el espacio-tiempo (donde como analogía se podría imaginar el espacio-tiempo como una cama elástica, donde los cuerpos pesados hacen que ésta se deforme y por tanto los objetos que pasen por ahí se desvían de sus trayectorias originales).
Masa inercial y masa gravitatoria: principio de equivalencia
Otro gran problema que traía consigo esta teoría (y que sirve como uno de los postulados desde los que se desarrolla la Relatividad General) es el conocido como principio de equivalencia. Éste aboga por el hecho de que en la Teoría de la Gravitación Universal se utiliza una cantidad propia de cada cuerpo que es la que origina la fuerza de la gravedad, su masa. Aunque aquí se ha relacionado directamente con la masa propia de cada cuerpo, ésta realmente podría ser definida como una masa gravitacional, en contraposición con la masa utilizada en la segunda ley de Newton, que habla sobre la inercia de los cuerpos, 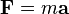 , y que podría ser llamada masa inercial. En la práctica, no existe ninguna ley, principio o hecho que establezca que ambas masas son, en efecto, la misma masa, como se ha supuesto en toda la descripción realizada (únicamente se conoce que ambas son prácticamente iguales con una gran precisión). Este hecho que traería una gran importancia, puesto que de no ser las mismas, la aceleración que experimenta un cuerpo dejaría de ser independiente de su masa por ejemplo, no ha podido ser resuelto de una manera efectiva, dando lugar al mencionado principio de equivalencia.
, y que podría ser llamada masa inercial. En la práctica, no existe ninguna ley, principio o hecho que establezca que ambas masas son, en efecto, la misma masa, como se ha supuesto en toda la descripción realizada (únicamente se conoce que ambas son prácticamente iguales con una gran precisión). Este hecho que traería una gran importancia, puesto que de no ser las mismas, la aceleración que experimenta un cuerpo dejaría de ser independiente de su masa por ejemplo, no ha podido ser resuelto de una manera efectiva, dando lugar al mencionado principio de equivalencia.
Véase también
- Gravedad
- Isaac Newton
- Campo gravitatorio
- Leyes de Kepler
- Teoría de la Relatividad General
- Fuerza G